novoMiRank tutorial

novoMiRank is a tool for comparing features of novel predicted miRNAs to a set of known miRNAs in the miRBase. Since in later miRBase versions the increase of miRNAs derived from NGS data and prediction tools is noticeable, we provide with our tool a way to compare user-defined novel miRNAs to e.g. early miRBase versions and rank the user input miRNAs according to their distance from the distribution of the selected reference miRBase versions. For this task, we defined 24 sequence, structure, and distance features as follows:

• base composition (percentage A,C,U,G) of precursor, 5p-miRNA, 3p-miRNA -> 12 features
• minimum free energy as computed by RNAfold 2.1.9 with parameters

  -d2 --noLP

  -> 3 features
• length of precursor, 5p-miRNA, 3p-miRNA, loop length -> 4 features
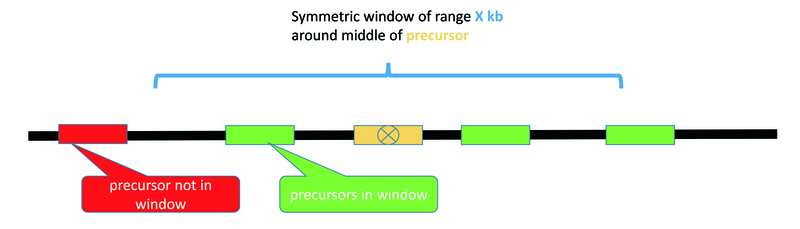
• distance to next precursor, numbers of precursors in windows of 5 kb, 10 kb, 50 kb, 10⁶ kb -> 5 features

For your convenience we provide two input types:

• 1) single precursor version: input of the sequences and location of one novel miRNA precursor

• 2) batch version: upload of a GFF file with annotations of your novel miRNAs/precursors

A GFF file is a tab-separated plain text file that is a standard format for sequence annotations. We use the GFF version 3, which is also used by miRBase. Here, you find additional information for the GFF3 format. Format description of a GFF file as novoMiRank expects it:

Some notes if you use the GFF upload function:

• We use the GRCh38 genome, so your GFF file must contain GRCh38 coordinates
• We discard precursors that have only one mature form annotated
• The distance and precursors in window computation is done by comparing your input to the locations of all 1,881 known current human precursors from miRBase v21 (including those having only one mature form annotated)
• The distance to the next precursor is computed from the genomic start position of the precursor to the start position of the nearest precursor on the same chromosome up-stream or down-stream neglecting the strand information
• The numbers of precursors in a window of size X kb is computed from the middle of the precursor and adding/substracting X/2 of the window size

• We trim the precursor to the start and ending of its mature forms, since the 5p and 3p overhangs are often very arbitrary